Un modelo matemático que puede explicar la dinámica social de un país Recibido: /enero, 2020. Aceptado: /marzo, 2020.

Abstract

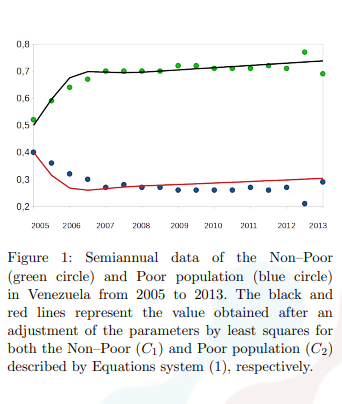
El presente trabajo presenta un modelo matemático que permite describir la desigualdad social de una población a lo largo del tiempo. Para realizar ello, la población de una nación o región se debe dividir en dos grupos sociales diferentes que serán etiquetadas como “Pobres” y “No Pobres”. Un primer modelo es aquel donde los grupos sociales no interactúan entre sí. Más tarde probamos otro modelo donde las personas No Pobres ayudan a las personas Pobres sin ningún tipo de retribución económica. Ambos modelos son estables en el tiempo. Finalmente se corroboró dicho modelo con los datos obtenidos del Instituto Nacional de Estadística de Venezuela desde 2005 a 2013.